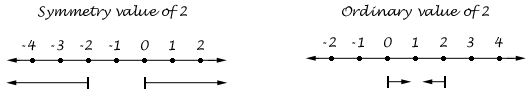A Primary Mathematical System

What is the largest number you can think of, no wait, what is the largest number of all? What is the total sum of all numbers? Of course the answer is that there isn't an answer to this question. But let's put it another way. What is the greatest universe of all? What if we imagine all things that exist? Can we at least find a single concept, a simple word, that includes all things combined together into one single whole universe? Is there such a word? Sure, this is easy. The word everything does that. Also there are words such as Universe, or existence, or being, which can be meant to symbolize everything that exists.

What about math? How many numbers in mathematics symbolize an everything in the number world? Is there some place on the real number plane which symbolizes the sum or the whole of all numbers? Interestingly, the answer to this question is no. As everyone knows, there is always a next greater number when counting and it isn't possible to count to a final largest number. There is just something different about the nature of the system of mathematics which makes it impossible for it to represent itself as a whole.

We could use the term positive infinity to refer to all the positive numbers combined together, but such a term would not actually represent a completed sum or combined whole. Since there is always a next greater number in this group there cannot be a single definite value. This positive infinity is more a representation of a never ending process; a series of numbers, and not a number itself. Of course the same is true of the infinity of negative numbers. Like the positive side, there isn't a unified sum of all the negative numbers.

But what if we combine together all the positive numbers with all the negative numbers? We can write this as an equation. At first it seems like if we try to sum all numbers into a single ultimate number; if we sum all the positive numbers with all negative numbers, then the total combination of all in question would sum up to zero, as shown below. 

(1 + (-1)) + (2 + (-2)) + (3 + (-3)) +... = 0 + 0 + 0 + ... = 0

Wouldn't that be strange if the sum of all numbers somehow equaled zero. We could then say that zero represents the everything of math, couldn't we. And that really wouldn't make sense, because the meaning of zero is very related to the word nothing.

The equation above makes it seem like zero is the sum total of all real numbers. There is always a negative value for every positive value, as shown above with integers. However, there is a problem with the consistency of this approach. It is possible to sum all numbers several different ways, and the sum does not always have the same answer. Several equations sum all real numbers yet each yields a different product. The two equations below add up all integers but as you can see, they have different sums:

(1 + 0) + (2 + (-1)) + (3 + (-2)) + (4 + (-3)) + ...  =  1+ 1 + 1 + ...

next:

((- 1) + 0) + ((-2) + 1) + ((-3) + 2) + ((-4) + 3) + ...  =  (-1) + (-1) + (-1) + ... 

These two equations, and the first equation that equals zero, each include all integers in the equation, yet we find three different solutions to the same equation. It is the same problem. In these equations we are summing definite things or values, which holds us in the realm of the finite, where a definite quantity of things is greater than zero things. The equations above sum a definite series of values, they don't sum the whole, and consequently it is said in mathematics that the sum of all real numbers is undefined. Which really kind of makes sense. Otherwise, zero would be a mathematical nothing and an everything simultaneously. So to be consistent, in ordinary math zero represents nothing and there is no ultimate number that represents all numbers, because math is the counting of definite things. 

Zero cannot represent both nothing and everything in the same mathematical system of values, and as long as we remember that, we can discover a second mathematical system, very similar to ordinary math, and yet very different, because in this new system, zero represents a mathematical everything, which produces a whole other kind of math. And what is perhaps most interesting, is that in the same way that there isn't a number in ordinary math to represent everything, in this new system there isn't a number to represent nothing.

Zero as the Whole of All Numbers

It is said that the sum of all real numbers is undefined but logicians and mathematicians made a mistake in formulating the rules concerning zero. We tested the hypothesis that all numbers might sum to zero, using a mathematical system where the value of zero is pre-set to be nothing. In ordinary math, all values are relative to zero as nothing, so of course we would discover that all real numbers do not sum to zero. If it were not so, the logical consistency of mathematics would be destroyed.

Since we developed math to count definite things, and zero represents no things, it makes sense that we don't commonly switch into a system where zero is the sum of all numbers, although it can be done. It just can't be done half way. As the saying goes, it's all or nothing. Either we can see zero as every number or we can see zero as nothing. 

It is only logical, that a test of the value of zero has to be a genuine consideration of the value of zero. If we test zero as the sum of all numbers we must allow its usual value of "nothing" to change to a value equal to the summation of all numbers. Which means we assume zero to have a value greater than all other numbers. Do you see what I am saying? Its a bit radical. If we sum all numbers instead of cancel all numbers, we alter the entire value system, and suddenly we have what appears at first to be nonsensical. If zero is the greatest value; i.e., the sum of all numbers, what then is the value of the number one, or two? Which is greater, one or two, if zero is greater than both?

How can zero be greater than one? This sounds like nonsense. Or perhaps we are touching on something completely different which takes time and thought to adjust to. Naturally in order to find out we must explore some unfamiliar terrain. However, keep in mind, that we are not considering a change to, or something new in, ordinary mathematics. The mathematical system developed since the dawn of human reasoning functions in relation to the definitive world of things that we observe each day. That system counts things, and it is a valid system evidenced by its application to the physical universe. And yet it is noteworthy, even important, that we notice how that system cannot describe the universe as a whole, as words and our thinking minds can. In math as we count a world of things we count upward into an endless abyss of numbers. If we wish to understand and describe the universe with a mathematical system that is able to represent the universe as a whole, then we have to make a switch and see the world in an entirely different way. Remember the first equation:

(1 + (-1)) + (2 + (-2)) + (3 + (-3)) +... = 0 + 0 + 0 + ... = 0

The simplest most straightforward way of summing all numbers is to sum the equal but opposite numbers together as shown above. So for a moment we will imagine that the correct sum of all numbers does sum up to and equal zero. Except this means that we need to change the value of zero away from being "no" things. We need to treat zero as the largest value in the mathematical system which actually includes the two already vast infinities of positive and negative numbers. Suddenly zero has become an infinite whole that contains all other numbers. Every positive and every negative number on the real number plane is summing or combining together to form an ultimate number of absolute value. Obviously this is not math as we know it. This is a math without time, without process, a math of truly infinite values.

So we have made a dramatic change and the next step is to see the effect that changing the value of zero has had on the value of other numbers. If we are going about this bravely, as if we are imaginatively exploring a series of ideas, and so the brain is actually working, we notice that the values of other numbers have also changed, transformed in the same shift that we have taken with zero. Ordinarily the nothing of zero is a foundational axiom. Our foundation has shifted dramatically. What now is the value of one or two? 

If zero is seen to contain all other numbers, then logically all other numbers must have a lesser value than that of zero. If zero is the largest value, the only way there can be lesser values is if we remove some measure of value from the whole of zero. For example, suppose that we take away a (-1) from zero. What remains in the absence of that (-1)? Zero is still very large but zero is no longer an absolute value containing all other numbers. Something has been removed from it. But what value does zero transform into to show that loss? 

The answer is simply that zero minus (-1) equals 1. The missing (-1) causes zero to transform into the value 1. If zero contains all numbers within it, and we take away a value, zero then contains all numbers except the removed value. If we remove a negative one from zero the value of zero records that loss by transforming into a positive one. It still contains all other numbers besides (-1). So it is still a very large number like zero. But it is no longer the complete whole of all numbers. It is one. A very large number one.

So if we treat what just happened as the logical rule we can now discover the values of other numbers in this system. For example, one is the sum of all numbers, so it contains within it all numbers, except (-1) is removed. The number two is the sum of all numbers except (-2) is missing, so it is also near zero but its content is less than zero and less than one. The number three contains all other numbers except (-3) so it is very large but smaller than two, one, and zero. And so on, and so on. The transformation that has happened is not simply an inverse reversal of ordinary mathematics, rather in this mathematical system, the value of a number decreases as we count toward greater numbers, since more of the negative numbers are being removed and placed somewhere else. 

Now, I should point out, just for the sake of clarity, that switching to the negative, the number (-1) is a combination of all numbers except that a positive 1 is removed, which would otherwise create the balance of zero. And in removing a positive two the whole shows that loss by becoming the number (-2). Unlike ordinary math, where negative values are less than nothing at all, here the numbers (-1) and (-2) are very large. In fact the content of (-1) is equal but inverse to the content of (+1). In physics, matter and anti-matter particles are equally substantive yet inverse in form and structure. 

Of course this feels odd to anyone at first exposure, and to a mathematician who is learned and naturally entrenched in the extensive field of mathematics, all this likely seems absurd and useless. Hopefully everyone is interested in and fascinated by logical consistency, and maybe wise enough to not expect to immediately see how a new set of ideas can be applied for some practical purpose. Keep in mind that we are no longer counting finite things, so it is certainly not being meant here that two things are less than one thing. None of this applies in any way similar to how ordinary mathematics is applied to the world in which we live. In what I shall now refer to as Symmetry Mathematics, the number zero is considered to be the everything of math. It is a complete and infinite value. In this system, there is a whole, and this means that the infinity of possible values is absolutely definitive, a definitive zero (like the physical reality of empty space), not merely a endless series or a process. In this new system zero is genuinely infinite, and as we remove a part from the infinite whole, we create definitive values which are themselves infinite as well. I can assure the reader that the applications of this system are as interesting as this system is unique. We can visually express this new system with the image below which shows the value or content of the number 2.

2|equals the set of all real numbers except (-2), or (-1)+(-1). The symmetry value of 2 can be drawn on a number line as shown.

It should be noted that we are not merely reversing the general value system of mathematics, we have changed the very nature of the system. This is most evidenced by the fact that there isn't any number in this system that represents nothing (and especially non-existence). There is no basic duality of something/nothing like that which exists in ordinary mathematics. An empty set in this system is recognized as the ultimate combination of all sets. And naturally, the values on either side of zero are less than the whole set. 

There exists two entirely different ways of seeing zero and all other numerical values. It is a whole other type of value system, a system as valid as the one we presently use, one of no use within the abstract world of individual things, yet immeasurably valuable in cosmology where a mathematical value for the universe as a whole is of critical importance in any attempt to understand for example, the implications of a universe in which space is flat and infinitely extended, not curved into a loop (discovered by the WMAP space probe), or the many worlds theory based on quantum mechanics. 

This new mathematical system is based upon a holistic perspective, its foundational axiom reflecting the innate singleness and wholeness of existence. Applied to the universe it would indicate that what we think of as empty space is really full and not empty. It would indicate that our universe is like a symmetry math number, definite, and yet infinite, but not yet the total infinite. Our universe is like the surface of the ocean, and underneath that surface is the rest of the infinite whole. Most importantly, it would show the interconnectedness of what we think of as separate things. As a perspective symmetry math doesn't see isolated or separate objects. Although its values are definitive, it does not see finite things. In the same way that its mathematical values are a combination of other numbers, this system represents physical form only as a single unified pattern, with each pattern (each number), being less than the whole. In the way that each number contains other numbers in symmetry math, a number is like a possible static state, a state being another term for a pattern. 

One shouldn't assume this unique value system threatens our normal value system in any way. Each is built upon a perspective. Two apples are still more apples than one. We can still divide up and see the world from a finite perspective, in which case the infinite can be seen only as an indefinite process. Symmetry math shows us that the infinite is real and exists in a realm greater than our sense of time and place., What this system does, is allow a radical shift of perspective, so that we can also see the universe as an undivided whole, where apples are part a single universe. In symmetry math, one of the conclusions we can draw is that for there to be a positive two apples (matter), there must be a negative two apples (anti-matter) removed from the pattern that we observe. Finite form requires that the two positive apples are less than the whole of the four apples combined.