| ||||||||||||
"
You cannot conceive of the many without the one."— Plato
From The Book:
Everything Forever:
Learning to
See Timelessness
"Whilst the world is thus dual, so is every one of its parts. The entire system of things gets represented in every particle. There is somewhat that resembles the ebb and flow of the sea, day and night, man and woman, in a single needle of the pine, in a kernel of corn, in each individual of every animal tribe. The reaction so grand in the elements is repeated within these small boundaries…"
— Ralph Waldo Emerson
"The electrons in a carbon atom in the human brain are connected to the subatomic particles that comprise every salmon that swims, every heart that beats, and every star that shimmers in the sky. Everything interpenetrates everything, and although human nature may seek to categorize and pigeonhole and subdivide the various phenomena of the universe, all apportionments are of necessity artificial and all of nature is ultimately a seamless web."
— Michael Talbot
"Frequently consider the connection of all things in the Universe. ... Reflect upon the multitude of bodily and mental events taking place in the same brief time, simultaneously in every one of us and so you will not be surprised that many more events, or rather all things that come to pass, exist simultaneously in the one and entire unity, which we call the Universe. ... We should not say ‘I am an Athenian’ or ‘I am a Roman’ but ‘I am a Citizen of the Universe'."
— Marcus Aurelius
"According to the movement of reason, plurality or multitude is opposed to unity. Hence, it is not a unity of this sort which properly applies to God, but the unity to which neither otherness nor plurality nor multiplicity is opposed. This unity is the maximum name enfolding all things in its simplicity of unity, and this is the name which is ineffable and above all understanding."
— Nicholas of Cusa
|
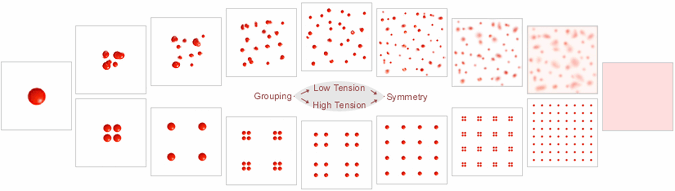
Grouping and Symmetry continued Grouping
Order Learning how all patterns inevitably evolve from one kind of order to another allows a person to see the single underlying process by which literally everything in the universe changes and evolves, including how we ourselves inevitably grow and change as individuals and as a society. As a first step toward seeing this basic evolution of nature we must recognize that disorder is a temporary stage between one order and the other. In the first four squares below we recognize a common portrayal of order becoming disorder. Similar to an opened flask of gas, in the decay of grouping order a single dense object breaks apart and begins to spread evenly. As with a gas, eventually the parts spread out randomly within the volume of the square. The order of the single object has seemingly disintegrated into disorder. However, we can also see below that in the overall spectrum of patterns the first four stages have been moving in the same direction toward the objects being perfectly balanced within the space of the square. In the first four stages the patterns have not only been evolving toward disorder, they have also been evolving toward symmetry order. Beyond that fourth stage exists the extreme of the objects being evenly spaced, which exists beyond what we think of as disorder. In the fifth stage, beyond the even spacing of objects, exists the extreme of a final stage, where the individual parts are diluted and spread perfectly even. If a system continues in the direction of increasing symmetry order (balance) the objects become one with the reference frame (the volume of the square). The range of possible patterns includes two types of order, with extremes of each order on either end. This is true for the universe as well.
Figure 1: Symmetry
Order Exists Beyond Disorder. The typical way that we expect changes to occur involves order The purpose of this transition of patterns above is to show that even if disorder seems to increase, the evolution of patterns in that direction are invariably moving toward another kind of order. Disorder is recognized here only to be a stage in the overall transition between two orders. To understand why this temporary stage of disorder occurs, in the next step we will reduce the disorder to a minimum. In any fundamental study of patterns we must recognize that all patterns exist trapped between the two kinds of order, and every pattern exhibits measures of grouping and symmetry. Said more precisely, each pattern exhibits a measure of cooperation between each order which varies in intensity. If the intensity of both orders is high, then the pattern exhibits a high measure of both grouping and symmetry, which we call orderliness. The entire transition of patterns below displays very high intensity between the two orders so it is very orderly. That high intensity decreases the amount of irregularity (disorder) allowed in the transformation, making each stage appear ordered.
Figure 2: In this very
simple transition between grouping and symmetry the tension between the two orders is high, Notice that at each stage, between the extremes on each end, there is a high measure of both grouping and symmetry. Above we are seeing the same transition as shown in figure 1, except throughout the transition in fig. 2 the influence of each order is intense, causing the objects to remain grouped but evenly spaced. This maintains the objects in a lattice pattern. In looking at these patterns we can imagine the cooperation of each individual type of order intensely competing against one another. Notice the influence of each side is apparent throughout the transition, as if the invisible influence from the extreme order on each side is reaching all the way across to the other side. Below we see these same two transitions shown together, showing nature has two options when evolving from grouping to symmetry, one where the intensity of each order is very low and another where the intensity is high.
The more orderly patterns in nature are the product of the two orders competing or cooperating with one another. Orderliness is created when two orders strongly cooperate or compete, while disorder occurs when the two orders weakly cooperate or compete. In the images below, a field of grass forms a large group of that plant and yet the even distribution of the grass in the field is symmetry order. An orchard or a grove is a group of trees while the trees are spread evenly, extremely even in an orchard, and less intensely even in a natural grove of trees where the competition between both orders is at a natural level.
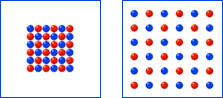
Thus far we have only considered the transformation of grouping to symmetry of a single element or one color. The same transformation using two colors is unique in that it requires a much more pronounced stage of irregularity. The patterns below portray two groups transforming into a single pattern of symmetry order. In order for balance to increase the two groups blend together, like the beginning moves of a chess game. This two color transition applies importantly to the small world of atoms since ordinary matter is created from positive and negative particles. With blue and red representing positive and negative, the end result of blending together is the neutrality of empty space, since oppositely charged particles annihilate one another. In the final stage the parts have enfolded into the perfect symmetry of space. They have become one with their reference frame.
Phase Transition I
always use a checkerboard pattern to represent symmetry order however that pattern is actually a limited measure of
symmetry order, since each square or circle in the lattice pattern represents a measure of grouping order, meaning that
we can divide up each square of our checkerboard pattern into smaller, finer squares and then mix them back together
again as a finer checkered pattern. Each square is unavoidably a grouping of smaller squares. Notice that once the
transition above reaches a stage where the objects are spread evenly, they must then divide apart or dilute in some way,
necessarily so if the pattern is to continue in the direction of increasing symmetry order or balance. In science this
would be called a phase transition. Importantly, note also in the two images to the right how an even distribution of the dots spread throughout the entire frame of reference (the square), has much greater symmetry order than a tight group of dots. The pattern on the left has greater grouping order, but the pattern on the right has greater symmetry order. The reason is because the even distribution within the reference frame is a more balanced pattern. Surprisingly, contrary to our ordinary sense of increasing order, symmetry order increases as parts are spaced or spread evenly throughout the entire reference frame. As we push the checkerboard pattern toward the ultimate extreme of its order the colors unify with the space itself, which exemplifies what always results from extreme symmetry order, a oneness of all objects and properties. Many different qualities or properties become one property. The final state is a unification of many things into a oneness that we ordinarily recognize as nothing at all, a perfect uniformity scientists sometimes refer to as a singularity.
Figure 7: Grouping and Symmetry Order with increasing color dimensions. In figure 7 above we see simple examples of rows, rings, and spiral, in this case portraying colors of light projected on a screen, forming patterns in which we easily see both grouping and symmetry. The first image of each example shows a grouping extreme while the last image shows the light combined together, resulting in a total lack of differentiation and form, yet each is the extreme of symmetry order for these patterns. Of course subjectively one's instinct abhors the notion of loss of form, the thought is almost horrifying to our identification with form, even if the separate forms are becoming the oneness we otherwise sometimes idealize. In reality we are more apt to see oneness as nothing. More objectively one's intuition might recognize that what is generally occurring in these transformations is that imbalances are combining together to become a balanced whole. There are many dualities in nature that balance out to zero, just as there are triads that balance out, and so on. Colors of light are an ideal example, in how the infinity of colors all sum to white light.
Figure 8: We observe simple grouping order and symmetry order in both galactic structure and atomic orbitals.
Fundamentally we know that all identifiable material things are non-zero imbalances. They are made of positives and negatives. And of course the ultimate balance point is always a zero balance. In science we describe the grouping of matter, stars, galaxies, planets, gases, as order, yet each represents an imbalance in nature. Here we are discovering that the balance of zero has to be considered a type of order also. Balance isn't a nothing, at least not in the sense of not existing. Real nothings are simply balances and uniformities. The absolute zero of physics is the ultimate balance, it is a combination of all times and places and things that collectively form a oneness, making the uniform result appear to be empty of things. A really amazing fact about the universe is that empty space, and the result of combining everything together into a unified whole, have the same exact qualities. So how then do we distinguish between the ultimate everything of symmetry order, and the nothingness of empty space? Actually there is no distinction. Even the ordinary empty space that surrounds us is far from empty. It is full. The world of things we exist within is not more than a primordial nothingness, but rather all we know is less than a timeless everything. Enfoldment Symmetry order is the unifying force in nature. It is the great attractor, the great point of balance toward which all change naturally progresses. Symmetry order is the invisible backdrop, the blank canvas, the board on which the game is played. But acknowledging symmetry order is far more involved than simply recognizing that balance leads to a smooth uniform pattern. The direction of symmetry order is not merely toward a balance between the objects we see in our universe. Such is simply what exists at the surface of symmetry order, like waves on an ocean. True symmetry order involves unification of the world we see with the complete world, the infinity of other worlds, of other times, and other lives, all of which must be in balance in order to not be a part of our world, because our world, the things of our world, are created from imbalances. Parts are removed from what we experience, anti-matter for example. For us to have form, our identical opposite anti-matter selves have to exist somewhere else, creating the imbalances we see as the finite world. And naturally imbalances tend toward balancing out. That is a universal principle we all recognize. And of course the final product of balance is the native state of the collective Universe, the timeless whole, the basic nature of existence, the default of being. In the direction of increasing symmetry, the form of objects of this world are fusing and combining together with the underlying balance of the timeless infinite whole. The physicist David Bohm called this process enfoldment. A surprising number of others in the past have constructed similar models of two orders, including Henri Bergson and William Yeats in the early 1900's, but the most recent and most notable was Bohm. Many of these same ideas were introduced by Bohm to modern science in the 1960's. In an interview with Omni magazine conducted by F. David Peat and John Briggs, David Bohm explained his concept of enfoldment: "Everybody has seen an image of enfoldment: You fold up a sheet of paper, turn it into a small packet, make cuts in it, and then unfold it into a pattern. The parts that were close in the cuts unfold to be far away. This is like what happens in a hologram. Enfoldment is really very common in our experience. All the light in this room comes in so that the entire room is in effect folded into each part. If your eye looks, the light will be then unfolded by your eye and brain. As you look through a telescope or a camera, the whole universe of space and time is enfolded into each part, and that is unfolded to the eye. With an old-fashioned television set that's not adjusted properly, the image enfolds into the screen and then can be unfolded by adjustment." Bohm did mean for implicate and explicate orders to replace order and disorder, unfortunately, the mainstream of other scientists didn't catch on to his vision, and Bohm struggled with despair and depression at not being able to convince the scientific community of the scientific value of his discoveries, a struggle I indirectly inherited and share frustration in. After independently discovering two orders in my own way, and learning to present my own system of seeing the same thing, the same principles, the same process in nature, and then discovering and studying Bohm's work in greater detail, I now believe the only reason Bohm's ideas were kept from having greater impact is that he was led more to challenge how quantum mechanics was being interpreted in his day rather than led to directly challenge the second law's usage of the terms order and disorder. Although judging from my own experiences I am sure it would have taken years for the challenge to sink in to the often dull collective mind of science. As a practiced theorist I am personally aware of how developing ideas have a rhythm of their own, a way of emerging in various forms, and unfolding. The way they introduce themselves determines the direction they develop. Having discovered two orders as I did, as an exploration of the structure of possibilities, one of the most important lessons I convey perhaps uniquely, is that properties of balance and symmetry are derived from an entirely separate component of the patterns we find in nature, distinctly different than grouping, and that an evolution of explicate order becoming implicate order is taking place right in front of us. After learning to recognize grouping and balance as different orders we can observe any pattern and recognize the two separate components contributing to the order of the pattern. Since we don't yet recognize that increasing balance or symmetry order is the product of a special form of order, we incorrectly recognize for example the spiral features below as being properties somehow associated with grouping order, we see them as a product of the past, when such properties actually are related to the balance of the future. Eventually I shall explain that symmetry order is an order in our own distant future continually influencing the present.
Perfect Symmetry We
are not accustomed to recognizing the simplicity of uniformity and sameness as being properties of an underlying
order. We all know that if we mix two or more things together to extreme they become one thing, but when that one thing is everywhere and everything, it looks like nothing at all, so it is difficult to rationalize that the original parts that went into creating the uniform pattern are still there in the uniformity. There is a similar uniformity and sameness in grouping order when we combine all of one kind of thing into a single object, like many atoms of gold together form a larger body of gold. But the combinational sum of like things creates a larger object with increasingly distinct and pronounced qualities relative to other things. In contrast, when all things combine together into one thing everywhere there isn't anything else to relate the sum of all to, so symmetry order is ever less pronounced as various qualities merge together. Of course this is not how we expect the world to add up. In math when we add up things the sum gets ever larger and pronounced, not increasingly more invisible. It seems of course that mixing different things together creates disorganization, at least in respect to the order we are so much more accustomed to. Causing the physical structure of things to disintegrate is not commonly seen as an alternative method of creating greater order. Disorder seems an end on to itself. Disorder seems like a general type of pattern with its own extreme measure, when in fact all disorder is a product of the two orders. Disorder is just an irregular combination of the two orders, small measures of grouping contrasted with small measures of evenness, arranged irregularly. The extreme of chaos can be understood as having a negative tension between the two orders. In other words, it takes work or effort to create high irregularity, which is why we observe so much order and only mild irregularity in our environment Advanced
Study:
Grouping and
Symmetry in Art and Nature Part Three: The Space of All Possibilities This essay last updated July 7th, 2007 | ||||||||||||||||||||||||
| Your welcome to send an e-mail and share your thoughts when you're done reading. |
|
Homepage | Part One | Part Two | Part Three | Part Four | Part Five | Contents | Backward | Forward | |
|
© Gevin Giorbran, Copyright 1996 - 2007 All rights reserved. Privacy Policy | Usage Policy |
"
All are but parts of one stupendous whole."— Alexander Pope
|
|


 Part
Two - Page Two
Part
Two - Page Two

























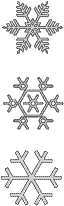 We
easily recognize the balance and symmetry in the pattern of a snowflake as being highly ordered. Yet the same
qualities of symmetry and balance pushed to extreme leads to an indistinct sameness that we have
no respect or appreciation for because of our identification with finite form. The funny thing is that when
many things become one thing, we see nothing. We are so attuned to recognizing the organizational properties of
grouping order, or the pattern complexity that results of patterns which utilize both grouping and symmetry, that the
uniformity of symmetry order in extreme, the order of oneness and wholeness, doesn't seem like anything at all.
We
easily recognize the balance and symmetry in the pattern of a snowflake as being highly ordered. Yet the same
qualities of symmetry and balance pushed to extreme leads to an indistinct sameness that we have
no respect or appreciation for because of our identification with finite form. The funny thing is that when
many things become one thing, we see nothing. We are so attuned to recognizing the organizational properties of
grouping order, or the pattern complexity that results of patterns which utilize both grouping and symmetry, that the
uniformity of symmetry order in extreme, the order of oneness and wholeness, doesn't seem like anything at all.